Comètes et Planète X (suite)
Article à revoir.
J'ai reçu des critiques intéressantes suite à la publication de cet article (ainsi que sa suite) qui m'incitent à le revoir en profondeur.
Je n'ai pas encore eu le temps de prendre en compte ces remarques. Aussi, en attendant:
1- par souci de correction, je me permets de reproduire ces remarques à la fin de cet article.
2- je ne vous incite pas à lire cet article, si ce n'est pour ... mieux critiquer :)
Je remercie vivement tous ceux qui contribuent à apporter leurs précisions. De mon côté, j'ai hâte d'essayer de nouvelles simulations dès lors que je trouverai un peu de temps. Merci et encore merci donc !
Cet article fait suite à un autre qui posait la question de la présence d'un corps gravitationnel massif à 120° d'inclinaison par la présence d'un excès de densité des comètes à trajectoire hyperbolique. Les tours et détours de cette recherche semblent conduire à des chemins inattendus...
Si vous avez lu l'article précédent, vous vous souviendrez que j'en étais arrivé à constater, suivant des paramètres orbitaux qui ne disaient rien de la distance ni de la position, un excès de densité cométaire provenant d'une région circulaire du ciel. L'ensemble des valeurs médianes obtenues étant les suivantes:
- Inclinaison ~ 120°
- Longitude du noeud ascendant Ω ~ 62.3°
- Argument du périhélie ω ~ 175°
Ces valeurs rejoignent celles de l'article de 1999 de J.B Murray, Arguments for the presence of a distant large undiscovered Solar system planet
Les choses devenaient intéressantes, mais comment les vérifier ? N'étant pas un spécialiste du sujet et n'ayant que trop peu de temps à investir dans des ouvrages, je me suis dit que le plus court chemin serait la simulation...
Sommaire
- 1 Densité du flux cométaire suivant l'inclinaison
- 2 Retrouver la fonction de densité de flux cométaire
- 3 Simuler un corps massif traversant un champ cométaire (à peu près) homogène
- 4 Un modèle pour le système solaire ?
- 5 Un modèle pour le soleil et son environnement galactique ?
- 6 Un modèle pour les nuages protoplanétaires ?
- 7 Remarques sur cet article
Densité du flux cométaire suivant l'inclinaison
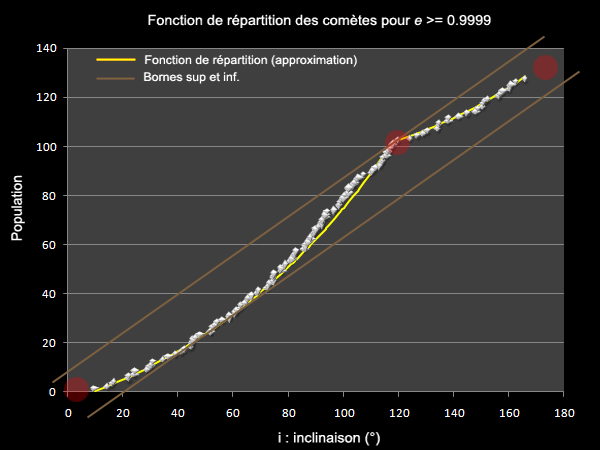
Avant cela toutefois, ma première démarche a été de dériver la fonction de répartition qui jusqu'alors présentait le nombre cumulé de comètes suivant l'inclinaison. Cette fonction est particulièrement intéressante car c'est elle qui montre pour les comètes à trajectoire hyperbolique, une extinction de leur nombre lorsque l'on se rapproche du plan de l'écliptique, et un accroissement notable autour des 120°:
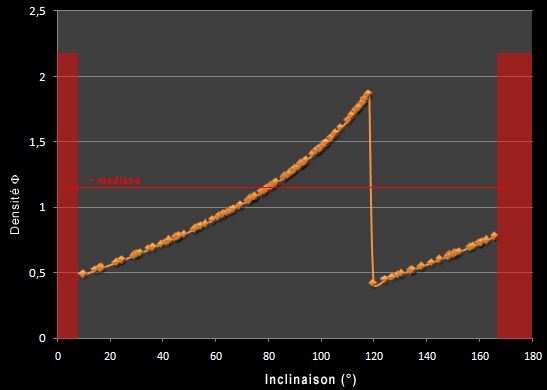
Dériver cette fonction permet en effet d'obtenir une lecture directe du flux cométaire en fonction de l'inclinaison, à contrario, le graphe ci-dessus se lit en cumul. Pour ce faire, je suis parti de l'équation par parties que j'avais utilisé pour modéliser la répartition (tracée en jaune). Celle-ci est constituée de deux morceaux d'arcs d'une même ellipse de paramètres a=3, b=2 (je vous passe les détails, mais ces paramètres avaient été déterminés par approximations successives et réduction d'erreurs, il y avait peut-être de meilleures fonctions d'approximation basées sur des fonctions de puissance ou d'exponentielle: je suis preneur). De là, l'expression de la dérivée s'obtient assez naturellement et le graphe de densité est le suivant:
Retrouver la fonction de densité de flux cométaire
A partir de là, il était légitime de se demander quel modèle constitué :
- d'un soleil,
- d'un corps Px, et,
- d'un nuage cométaire,
pouvait permettre de créer une telle fonction de densité de flux ?
Autrement dit, comment, une éventuelle planète X qui traverserait un nuage cométaire situé aux confins du système solaire pourrait nous "arroser", de façon que de la terre nous observions une telle répartition ?
Il me semble que deux principaux types de facteurs doivent être considérés afin de pouvoir reconstituer une telle fonction de densité :
1. La structure du nuage cométaire
La structure du nuage cométaire traversé à savoir: sa distance, épaisseur, fonction de densité... Si nous considérons qu'il s'agit du nuage d'Oort, les données existantes à son sujet, sont malheureusement que peu fiables à ce jour. Il est par exemple possible de considérer que la limite interne de ce nuage est située à 30 000 Unités Astronomiques (UA) et que sa limite externe est à 150 000 UA formant une coquille épaisse de 120 000 UA autour du système solaire. L'autre point c'est la fonction de densité des comètes suivant la distance de ces limites interne/externe qui peut être de différents types: loi normale centrée/réduite, loi normale asymétrique, constante par parties (à savoir, densité homogène importante en dedans, et homogène faible en dehors), linéaire par parties, etc. : il y a de quoi s'amuser (!)
2. Les paramètres orbitaux du corps traversant
L'autre aspect, concerne la trajectoire de ce corps: son orientation va déterminer le flux renvoyé vers le soleil. De façon intuitive, nous percevons bien que l'orientation qu'aura ce corps vis à vis du soleil sera importante:
- dirigé vers le soleil, le flux cométaire qu'il projettera vers nous sera intense,
- allant en direction inverse, nous devrions être relativement "protégés", néanmoins un reliquat arrivera toujours jusqu'à nous.
En toute logique en croisant 1. et 2. nous devrions pouvoir reconstituer la fonction de densité. La plus grande difficulté soulevée me paraissant être celle de l'évaluation du flux cométaire projeté par un corps massif traversant un champ de petits corps: à quoi pouvait bien ressembler une telle projection ?
Simuler un corps massif traversant un champ cométaire (à peu près) homogène
Ce genre de simulation a certainement déjà réalisée car elle est très simple. Le programme proposé ci-après (en php) est relativement compact. Il utilise les paramètres suivants:
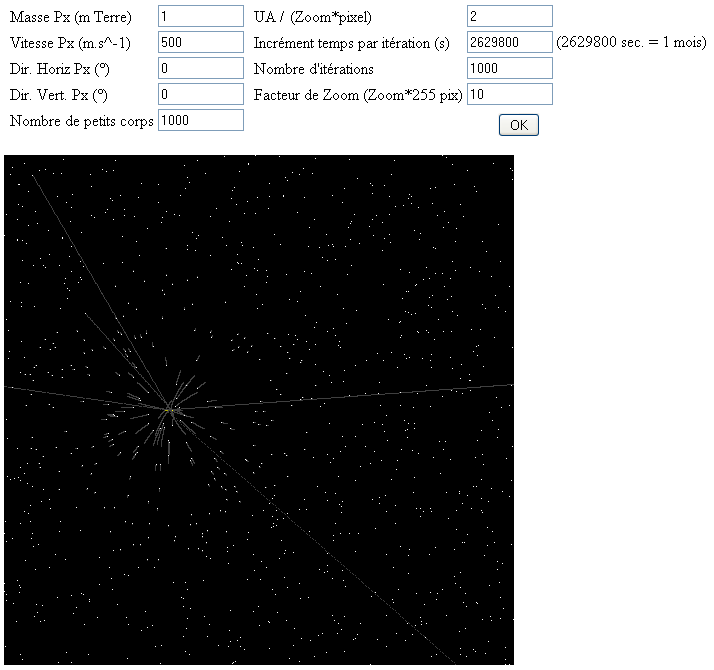
#mX masse de la Px, en masses de la terre #vX vitesse de la Px, (m.s-1) #aXh direction horizontale de la Px, (°) #aXv direction verticale de la Px, (°) #nb nb de petits corps (comètes) pris pour la simulation #UAPix Facteur d'échelle espace, UA / (pixels*niveaux de zoom) #kTa Incrément de temps pour chaque itération de la simulation (en années) #It Nombre d'itérations de la simulation #zF niveaux de zoom du graphique en multiples de 255 pixels
Mise à part la durée des itérations, j'ai rapporté ces paramètres à des échelles de temps et d'espace suffisamment grands afin que l'observation soit compatible avec l'échelle du système solaire. Je n'ai pas mis ce programme en ligne car couteux en calcul machine, cependant si vous voulez vous amuser, les sources des programmes sont donnés ci-après (remplacer .txt par .php):
Le programme permet aussi les simulations sur l'axe z, mais j'ai commenté les lignes concernées pour gagner du temps de calcul, (ce n'est vraiment rien à rajouter). A ce stade, je pense que les simulations qui vont suivre sont déjà relativement éloquentes.
La simulation ci-dessus, présente les paramètres par défaut du programme: simulation sur 1000 mois pour un corps de la masse de la Terre allant en ligne droite au travers d'un champ cométaire. Les petits corps n'ont pas de vitesse initiale. Le temps de calcul associé est d'une dizaine de secondes. Ce n'est pas très spectaculaire, on observe que le corps central a avancé de 8 pixels, (trajectoire jaune) et autant d'UA. Certains corps cométaires qui étaient trop près ont été éjectés à grande vitesse.
Premiers résultats
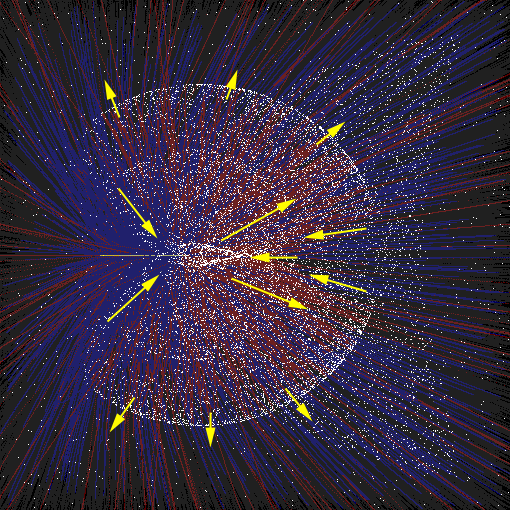
La première simulation que j'ai faite tourner n'utilise pas des paramètres réalistes, cependant grâce à elle il a été possible de disposer d'une image intéressante des phénomènes à l'œuvre:
Commentaires sur cette première simulation
- Le corps massif central se déplace de la gauche vers la droite. Sa trajectoire est tracée en jaune.
- Les trajectoires tracées en rouge sont celles des corps qui s’éloignent, en bleu celles des corps qui se rapprochent. Les flèches jaunes représentent les directions privilégiées de ces corps,
- La pression du vent interstellaire est négligée (le vent solaire n'est pas concerné, puisque nous sommes situés bien au delà!) : les petits corps représentent des masses suffisamment importantes, pour les corps cométaires connus, comprise entre 10^11 kg et 10^17 kg,
- Les nombreux corps détachés sur l’avant (en forme de queue de poisson) n'ont pas encore été "aspirés" par le corps massif. Il faut imaginer sinon que le flux serait continu par l'avant.
- Les corps sont, pour la plupart, éjectés sur les côtés.
- Sur l'arrière, il existe un espace de vide important. Cet espace existe également dans l'axe avant, mais moins important,
- Il existe une jolie “flamme de bougie” autour du corps central et dans son axe de déplacement. Ce faisceau en forme de flamme est créé à partir des débris collectés sur l’avant et l’arrière et qui spiralent dans l’axe du sens de déplacement.
- On observe deux bulles qui gonflent et se propagent. Ce sont des ondes à l'instar d'ondes qui peuvent être créées par un cailloux jeté dans l'eau, ou bien mieux, à l'image d'ondes sonores créées autour d'un véhicule en déplacement.
Un modèle pour le système solaire ?
Ma première réaction a été de me dire : l'image obtenue parait fournir une représentation approchée du soleil avec son nuage d'Oort et sa ceinture de Kuiper, étonnant! Est-ce à dire que ce qui valable pour une éventuelle planète X traversant un champ de corps en équilibre gravitationnel est aussi valable pour le soleil traversant le milieu galactique ?
Peut-être. Moyennant l'utilisation de paramètres compatibles, si cela permettait de fournir un modèle de la dynamique à grande échelle système solaire cela pourrait être riche d'enseignements : ordinairement, nous pensons que les corps du nuage d'Oort sont en équilibre gravitationnel autour du soleil. Or, là c'est tout l'inverse: le corps central ne retient pas autour de lui les petits corps rencontrés car ils sont complètement instables !
L'illusion d'une "bulle figée" concernant le nuage d'Oort est liée à des observations (parcellaires) se déroulant sur des échelles de temps trop courtes, pour ne pas dire instantanées. Ne disposant que d'une image arrêtée de ce processus, nous pouvons penser que les limites internes et externes de cette bulle sont stationnaires, mais ce ne serait pas le cas!
Le nuage d'Oort serait en réalité une onde qui met des millions d'années à se propager, se désagrégeant avec la distance ou bien lors que celle-ci ne serait plus alimentée. Qui plus est, c'est une onde qui serait entretenue, nécessitant que le corps central continue à traverser un milieu suffisamment riche en débris.
Ce modèle étant valable sous réserve, que :
- la densité de corps environnante soit suffisante, et que,
- la vitesse et la masse du corps central aient des valeurs précises. Nous reviendrons sur ce dernier point.
Implications
Et finalement, est ce que cela ne voudrait pas dire que les défauts de densité cométaire relevés précédemment trouvent leur raison dans la structure particulière du nuage d'Oort ? Peut-être bien. A savoir:
- Pour la direction horizontale
- Il existerait un déficit cométaire plus important sur l'arrière de la direction de déplacement du Soleil,
- Il existerait également un déficit cométaire moindre sur l'avant de la direction de déplacement du Soleil,
- Pour la direction verticale
- De manière générale, la densité cométaire serait augmentée sur 120° d'inclinaison compte tenu d'un flux galactique maximal dans cette direction.
Vérification du modèle pour la direction horizontale (plan de l'écliptique)
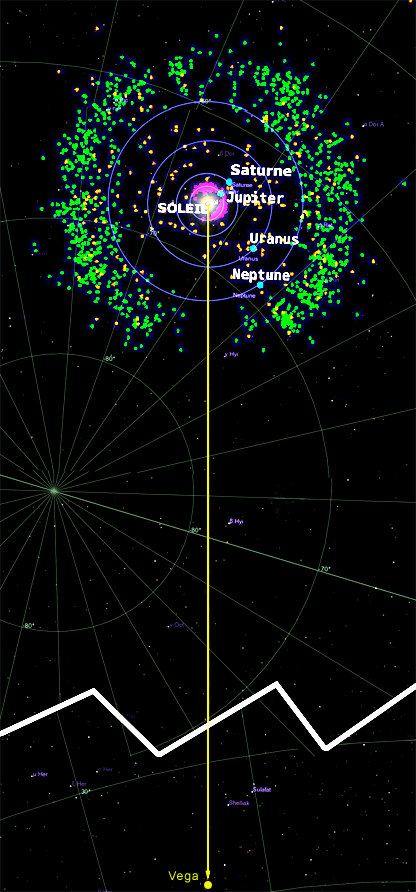
Une conjonction étonnante (mais à priori spécieuse) avec la ceinture de Kuiper
La première idée qui me vint consistait à rapprocher cette simulation de la forme particulière de la ceinture de Kuiper. En effet, cette dernière présente un déficit inexpliqué de TNO (objets Trans-Neptuniens) dans deux directions opposées de l'écliptique, dont l'une est notablement plus marquée que l'autre. Or, il s'agit précisément de l'une des caractéristiques importante de la simulation précédente.
Et toujours pour tenter de vérifier les "enseignements" de la simulation précédente, la direction de plus fort déficit pouvait-elle correspondre à la direction vers laquelle le système solaire se dirige ? (direction que nous appelons apex et qui correspond approximativement à l'étoile Vega). Eh bien, oui! Le hasard fait que la direction de l'apex et de la dépression concordent à la date à laquelle le positionnement a été réalisé, soit le 01/01/2000 :
Cependant il faut bien qu'il y ait une logique gravitationnelle à l'oeuvre: les orbites des objets Trans-Neptuniens modélisées par le Minor Planet Center (en rouge ci-dessous) font que la position de la dépression évolue elle aussi et effectue une rotation en environ 250 ans : plus question d'alignement avec l'apex ! - A moins que les trajectoires orbitales calculées pour les TNO soient erronées ce qui parait tout de même très improbable...
Cependant, objectivement, il existe un paradoxe (non résolu) dans l'existence de cette dépression: si les trajectoires des TNO sont bien circulaires, ceux ci étant disposés sur une surface en forme de disque, les plus proches du soleil auront une vitesse angulaire plus élevée: cela crée un mouvement de cisaillement dans la rotation. A l'échelle de l'animation ici proposée, nous le percevons bien: le trou observé disparaîtra d'ici quelques centaines d'années, et ce compte tenu des différentiels de vitesse angulaire. Aussi, quel "hasard" ( / phénomène) a pu faire en sorte qu'une telle dépression existe de nos jours ? Biais observationnel peut-être ?
Les autres anomalies connues de la ceinture de Kuiper
Il existe deux autres anomalies principales :
- La présence d'un nombre anormalement élevé de couples binaires de dimensions similaires. Cela semble exclure un modèle de formation par chocs. - Est-ce à dire que les couples se sont d'abord formés dans le milieu galactique et ensuite ont été attirés par le soleil ?
- Un déficit important de petits corps par rapport à des corps de masse plus importante - Peut-être que ces derniers ont pu pénétrer les couches internes du système solaire grâce à leur gravité, les corps plus légers étant plus sensibles au vent interstellaire ?
Apex et longitude du noeud ascendant Ω calculé (°)
[...à venir ...]
Vérification du modèle pour la direction verticale (inclinaison)
Nous avons traité l'orientation suivant le plan de l'écliptique, mais qu'en est-il de l'inclinaison?
A l'instar d'un rayonnement qui tombe sur une surface, l'intensité reçue sera d'autant plus élevée que la surface sera orientée perpendiculairement à ce flux. Il s'agirait ici de la même chose avec l'orientation que fait le plan de l'écliptique avec le plan galactique, déterminant l'intensité du flux de débris reçus.
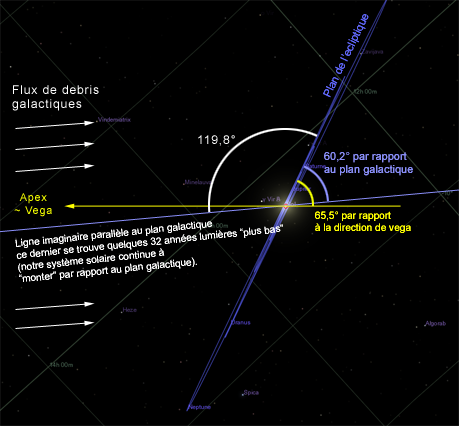
Rappelons nous que l'article précédent calculait un plan d'inclinaison de 120° pour le flux cométaire maximal (il pouvait même être très légèrement inférieur à 120°). Or précisément, le plan galactique est incliné de 119.8° par rapport au plan de l'écliptique: il serait donc tout à fait logique que dans cette direction du ciel le flux reçu soit plus intense !
|
Ainsi, si effectivement le nuage d'Oort est une onde alimentée par les débris galactiques, il s'agit là de l'élément le plus probant, montrant qu'il existe une relation directe entre le milieu galactique et le nuage d'Oort. Et, nous tenons alors une explication qui ne nécessite pas de faire appel à une "Planète X"!
Un modèle pour le soleil et son environnement galactique ?
Il est possible d'essayer d'appliquer les simulations précédentes au cas du soleil. Il faut toutefois considérer que ceci ne peut-être qu'indicatif. Ce genre de simulation est très sensible aux dérives linéaires (glissement progressif dans une direction) et circulaires (les orbites successives ne se recouvrent pas, comme si elles étaient en rotation).
Ces dérives causent malheureusement des incertitudes importantes sur les résultats des simulations. Il est facile de s'en rendre compte en réalisant deux simulations à priori équivalentes : réalisez une première simulation avec un nombre d'itérations élevé et une durée faible pour chaque itération; puis réalisez une deuxième simulation de durée totale identique, mais inversez les rapports: prenez un nombre d'itérations plus faible et une durée pour chaque itération plus importante. Au final, bien que les deux simulations soient de durées équivalentes, vous obtiendrez des résultats sensiblement différents ! Hélas...
Ces dérives ont plusieurs causes conjuguées :
- Les calculs sont basés sur le relevé de positions successives des planètes qui sont censées avoir chacune un mouvement propre. Ceci provoque une dérive linéaire. On pourrait théoriquement choisir des valeurs telles que le centre de gravité des deux planètes ne bouge pas.
- Chaque position est calculée à partir de la précédente ; les calculs ayant une précision nécessairement limitée les imprécisions de chaque boucle sont cumulées. Le résultat de chaque calcul comporte un certain nombre de chiffres ; les suivants sont perdus. Les erreurs agissent donc toujours dans le même sens ; proportionnellement aux nombre de boucles. Ce type d'erreur pourrait peut-être être évité en arrondissant chaque résultat au chiffre le plus proche au lieu de tronquer mais ceci nécessite une étude poussée des opérations de calcul en JavaScript.
- Le mouvement est considéré comme linéaire et uniforme entre deux boucles. La précision varie donc en raison inverse de la durée d'une boucle.
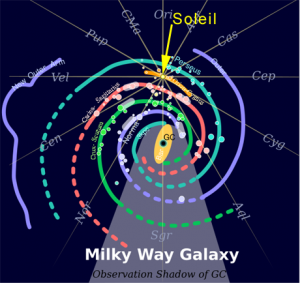
Pour revenir à la simulation concernant le soleil et son environnement galactique, le principal paramètre connu est sa masse de 1,99*10^30 kg. Concernant sa vitesse par rapport à l'environnement galactique immédiat, difficile de se prononcer. Le soleil se situe dans un bras galactique que nous appelons le bras d'Orion. Les résultats publiés en 2009 d’un suivi des étoiles les plus brillantes de notre galaxie par un réseau de 10 radiotélescopes, laissent penser qu’au niveau du soleil, la galaxie tourne à une vitesse de 254 km/seconde. Ce qui représente un différentiel de vitesse substantiel de -37 km/s : à priori, notre région galactique se déplace plus vite que le soleil. Mais cette mesure qui s'applique à des étoiles est-elle aussi valable pour un éventuel nuage de débris que notre soleil traverserait ? Rien de moins sûr... Ce qui est certain, c'est qu'un différentiel à l'échelle de kilomètres par secondes semble ne rien donner de probant en termes de simulation: pour obtenir un motif d'onde, le différentiel de vitesse semble devoir rester très faible.
| . |
La vitesse négative du soleil par rapport au milieu environnant, si elle se confirme, expliquerait également le fait que la principale brèche du système solaire soit orientée "à l'envers", c'est à dire au lieu d'être vers l'arrière du sens de déplacement, elle est vers l'avant, dans la direction de l'apex.
Mais que nous donnent les simulations avec une vitesse de quelques de dizaines de m/s et une masse équivalente à celle du soleil ? Retrouve t-on le motif en bulle avec des ouvertures asymétriques ?
Nous retrouvons effectivement un motif d'onde. La simulation ci-dessus, ne permet pas de mesurer la longueur d'onde car la deuxième onde n'est pas encore visible. Cependant, nous retrouvons bien les brèches avant / arrière, et une densité augmentée près du noyau central.
Il faut préciser qu'il n'était absolument pas évident qu'une onde "centrée" sur le soleil apparaisse. Pour preuve, voici une série de simulations à plus courte échelle de temps, et dont la vitesse de déplacement du corps central (masse du soleil) est progressivement augmentée:
Chose remarquable, à l'inverse d'une onde mécanique, plus la vitesse du corps traversant le milieu devient importante, plus l'onde prend de l'avance et est projetée vers l'avant.
Un modèle pour les nuages protoplanétaires ?
Il ne s'agit pas de résultats dans la mesure où des vérifications doivent être réalisées. Néanmoins, deux exemples de simulations semblent assez révélateurs de certains phénomènes que l'on peut observer dans le milieu interstellaire.
1. Sortie d'une zone de débris
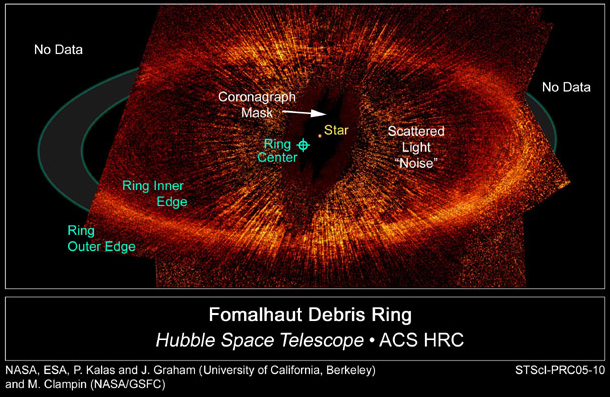
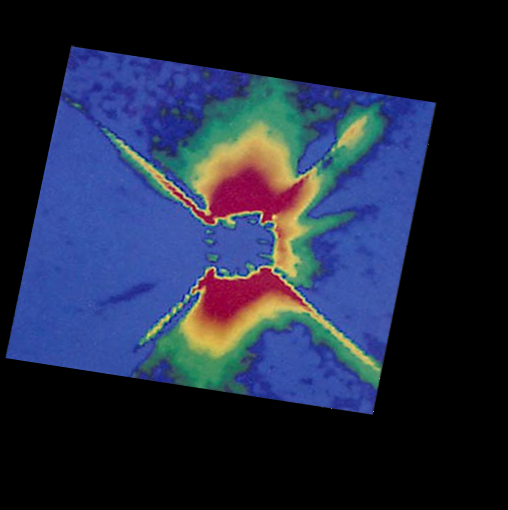
Que se passe t-il si la simulation continue jusqu'à épuisement du "carburant" constitué par les débris ? Par exemple, si l'étoile quitte une zone dense ou achève de disperser l'ensemble des débris de sa zone? Et bien, un profil particulier en forme d'ailes de papillons apparait. Curieusement, une photo de Beta Pictoris, mise à disposition par le CEA, nous montre un disque protoplanétaire de forme similaire. Je resterais néanmoins très prudent sur l'interprétation à en donner : le motif en croix parait être un artefact lié aux bras de support d'un miroir secondaire, de même que sur ma simulation le motif en croix est un artefact lié aux coins de l'image :

|
|
2. Nuage protoplanétaire non centré sur l'étoile
Alors que dans un modèle à orbites stables l'étoile centrale devrait être le centre de masse, de façon récurrente, il me semble que nous observons des nuages protoplanétaires dont l'étoile est décalée par rapport au centre du disque de débris. Compte tenu des simulations, cela est un effet lié à la vitesse de déplacement du corps dans le milieu galactique.
Remarques sur cet article
1°) Répartition des comètes paraboliques selon leur inclinaison
Le fait de trouver peu de comètes « paraboliques » à inclinaison voisine de zéro est un biais référentiel.
En langage courant :
- Les comètes provenant d’une latitude 0° peuvent avoir selon l’orientation de leur plan une inclinaison de 0 à 90°.
- Les comètes provenant d’une latitude de 90° auront une inclinaison de 90° et pas inférieure.
- Les comètes provenant d’une latitude de 40° n’auront pas une inclinaison inférieure à 40°.
En bref, ne pas confondre inclinaison et latitude de provenance.
Comme vous semblez très fort en simulation, faites la simulation suivante :
Répartissez de nombreux points d’origine des comètes en densité égale sur toute la surface de la sphère céleste. Pour chaque point, supposez des comètes (360) dont le plan varie de 1° (tournant autour de l’axe centre de la sphère, point d’origine de la comète). Calculez les inclinaisons et vous trouverez une courbe voisine de celle que vous essayez de décrypter. Il intéressera aussi d’avoir le résultat pour les deux autres angles (périhélie et nœud) pour savoir si l’un ou l’autre aurait aussi une distribution irrégulière
2°) Excentricité
Si l’on tient compte de la précision des trajectoires, aucune comète n’arrive avec une trajectoire hyperbolique. L’excentricité qui est donnée pour les comètes à longue période est celle de l’orbite osculatrice à la date du périhélie, c’est à dire ayant subi les perturbations dues aux planètes. Pour vos études vous devez utiliser le « 1/a d’origine » calculé avant toute perturbation par les planètes. En comparant les « 1/a d’origine » et les « 1/a futurs » (valeur calculée pour la comète sortante après toutes perturbations par les planètes) on constate pour les comètes qui arrivent « paraboliques » ou « quasiment paraboliques »
- 1/3 (environ) deviennent hyperboliques et seront éjectées du système solaire
- 1/3 voient leur 1/a inchangé à la précision des mesures
- 1/3 voient leur 1/a diminuer, la trajectoire devient plus elliptique, la comète aura droit à un prochain tour.
3°) Axes de recherche
Les deux remarques ci-dessus décrédibilisent totalement vos conclusions.
Il faut repartir de la base :
Placer les points d’origine des comètes « paraboliques » (= selon le 1/a d’origine) sur la sphère céleste (ou mieux sur la sphère galactique si vous voulez isoler l’effet des marées galactiques).
Déceler les zones de densité anormales.
Cela a déjà été fait : (voir image à la fin : Article de la revue « L’Astronomie » de nov 1989 de Delsemme)
En dehors de la ligne et du croissant dessiné la densité des comètes est la même.
Dans le croissant et dans la ligne étudier les particularités (Q angle du plan ) et par simulation voir si l’hypothèse passage lent d’une naine brune ou passage d’une étoile est confortée. C’est sans doute ce qu’a fait Murray dans l’étude que vous citez.
Bonjour,
[...] concernant l'hypothèse de la présence d'un corps massif dans le nuage de Oort.
De nombreux articles ont été consacrés à ce problème (voir de nombreux papiers par Matese, mais aussi Napier). De mon côté, bien que travaillant sur la dynamique des comètes, je n'ai jamais étudié ce problème. Pas par manque d'intérêt mais étant donné le nombres de difficultés dans la modélisation de cette dynamique, celle d'un corps massif dans le nuage semble être un des derniers paramètres à prendre en compte. D'autre part, toutes les études sur ce corps massif ne reposent pas sur des modèles dynamiques, mais plus sur des observations qui sont peu nombreuses et peu précises.
Il faut savoir par exemple qu'uniquement une meilleure modélisation des forces non gravitationnelles réduit le pic de Oort (l'endroit où s'accumule les demi-grand axes des comètes à longue période connues) d'environ 25 000 UA à 17 000 UA.
D'un autre côté des modèles dynamiques montrent que la plupart des comètes viendraient du nuage de Oort interne ( demi-grand axe inférieur à 10 000 UA, d'après un article de cet été de Kaib and Quinn dans Sciences).
Enfin, la survie ou la capture d'un corps massif dans le nuage de Oort pose des problèmes qui à mon avis sont plus importants que les résultats statistiques peu solides.
Tout ça pour dire que, si cette hypothèse ne peut évidemment être rejetée, travailler sur ce problème est périlleux. Ainsi, pour qu'une nouvelle étude soit justifiées il faudrait passer beaucoup de temps sur l'analyse des données, montrer que les accumulations observées ne peuvent être produites ni par la marée galactique ni par une éventuelle étoile passante, et montrer enfin qu'un tel corps peut survivre dans le nuage de Oort pendant 4.5 Gyrs (la capture récente étant trop improbable). Je n'ai malheureusement pas le temps de me consacrer à un tel travail.
Ceci dit votre travail est impressionnant. J'espère surtout que votre passion pour les comètes et leur origine va continuer.
Bien cordialement,
Bonjour
j'ai lu votre texte sur les comètes.
La recherche d'anomalies dans la distribution de comètes est très délicate. Il est très facile de se tromper.
Je pense que le point du départ de votre réflexion est affecté par une erreur induite par un piège de la géométrie. Une distribution isotrope, n'est pas une distribution uniforme par rapport à l'inclinaison orbitale i. Ceci parce que le volume de l'espace orbitale (i,Omega) entre i et i+di est proportionnel à sin(i)di. Donc, une distribution isotrope aura une distribution cumulée en cos(i). Je pense que, si vous tracez la courbe 63.5*(1-cos(x)) sur le graphique de la page 7, vous aurez un très beau fit de la distribution observée. Donc, l'inclinaison privilégiée de 120 degrés est illusoire.
La raison pour laquelle la distribution des comètes "vieilles" (celles avec e<0.9999) ne montre pas cette sinusoïde est que il y a un excès d'objets avec inclinaison voisine à 0 ou 180 degrés, car celles-ci sont les orbites le plus facilement défléchies par les planètes.
Je vous joint un article de Wiegert et Tremaine sur l'origine des comètes à longue période, ou toutes ces distributions sont discutées et reproduites dans une simulation numérique. Vous verres que toutes les distributions d'inclinaisons sont bien rapportées à des distributions plates en cos(i), et que la distribution de toutes les comètes a un excès d'objets aux deux extrêmes de la distribution (Fig. 3).
Quelque réflexion concernant les autres distributions que vous montrez:
Celle de la page 11 (le trou autour de Omega=62 pour les comètes avec i=120 degrés) est du au fait que le plan galactique a une inclinaison de 120 degrés par rapport à l'écliptique et une longitude du noeud de l'ordre de 60 degrés. Donc, les comètes avec i=120 degrés et Omega~60 degrés ont une inclinaison par rapport au plan galactique presque nulle. Or, il y a bien un déficit de comètes nouvelles de petite inclinaison galactique (voir figures 12 et 13 dans Wiegert et Tremain), car la marée galactique est nulle sur son plan.
Le diagramme en haut de la page 12, en revanche, peut être lu comme deux distributions uniformes en omega, une plus raide pour omega<180 et une moins raide pour omega>180. Je pense que ceci est du à un biais observationnel. Les comètes sont découvertes en majorite' au passage au perihelie, par des observateurs situés dans l'hémisphère nord de la terre. Ceci privilégie le cas omega<180 degrés.
J'espère de ne vous avoir pas trop decu. Je sais bien qu'il y a eu d'autres études sur la planètes X et son influence sur l'orbite des comètes (par Matese notamment). Aucun n'a jamais fait brèche dans la communauté. Comme le disait Sagan, "extraordinary claims require extraordinary evidence". Je n'exclue pas qu'il y ait une planète ou une petite naine brune aux frontières du système solaire, mais je pense que l'on na pas encore une "extraordinary evidence". Peut être ca viendra un jour avec PanStarr ou le LSST.
Bien amicalement